
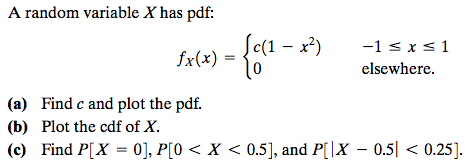
This is consistent with the formula derived above.To determine the distribution of a discrete random variable we can either provide its PMF or CDF.
#Finding cdf from pdf pdf#
Since the CDF corresponds to the integral of the PDF, the PDF corresponds to the derivative of the CDF:į X ( x ) = F X ′ ( x ) = d F X d x. Still, one frequently wants to make use of the probability density function f X ( x ) f_X (x) f X ( x ) rather than the CDF. Given a discrete random variable X, and its probability distribution function P ( X x) f ( x), we define its cumulative distribution function, CDF, as: F ( x) P ( X k) Where: P ( X x) t x min x P ( X t) This function allows us to calculate the probability that the discrete random variable is less than or equal to some. Note that it does not matter if the inequalities are strict (if the interval is or ( a, b ) (a,b) ( a, b ) for example): since the probability of any given value is zero, the endpoints can be included or not without changing any probabilities. P ( X ∈ ) = P ( a ≤ X ≤ b ) = F X ( b ) − F X ( a ).

Confused about where to start for each concept 5.
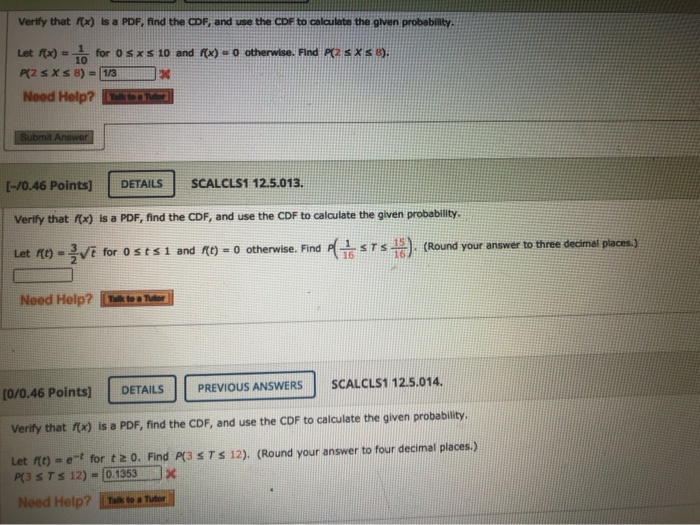
P(X \in ) = P(a ≤ X ≤ b) = F_X(b)-F_X(a). Calculating probabilites and finding CDF/PDF given information. P ( X ∈ ) = P ( a ≤ X ≤ b ) = F X ( b ) − F X ( a ). Instead one considers the probability that the value of X X X lies in a given interval: In the case of a continuous random variable, the function increases continuously it is not meaningful to speak of the probability that X = x X = x X = x because this probability is always zero. The functions with the extension cdf calculate the lower tail integral of the probability. The above example of Python processing PDF and CDF is all the content. Cumulative distribution functions of various distributions. Find cdf from pdf pdf Problem 6.2.1 Solution We are given that W X +Y and that the joint PDF of X and Y is fX,Y (x,y) 2 0 x y 1 0 otherwise (1) We are asked to nd the PDF of W.
#Finding cdf from pdf how to#
In the case of discrete random variables, the value of F X F_X F X makes a discrete jump at all possible values of x x x the size of the jump corresponds to the probability P ( X = x ) P(X = x) P ( X = x ) of that value. Find cdf from pdf how to Find cdf from pdf pdf The rst step is to nd the CDF of W, FW(w).

If x → ∞ x \to \infty x → ∞, this corresponds to P ( X ≤ ∞ ) P(X \leq \infty) P ( X ≤ ∞ ) which will be one because it is certain that X X X takes some finite value. This is because as x → − ∞ x \to -\infty x → − ∞, there is no probability that X X X will be found that far out if the PDF is normalized. of size-n random samples and compute Sn of each random sample and find out the. It increases from zero (for very low values of x x x) to one (for very high values of x x x). The following provides the CDF (left) and PDF (right) of an exponential. So the CDF gives the amount of area underneath the PDF between two points. P ( a ≤ X ≤ b ) = F X ( b ) − F X ( a ). Now, the probability is rewritten as the difference in values of the CDF: P ( a ≤ X ≤ b ) = ∫ a b f X ( x ) d x. Recall that previously this probability was defined in terms of a PDF: Using this definition, one can write the probability that X X X takes a value in a certain interval without using an integral. Which is the probability that X X X is less than or equal to x. For any random variable X, X, X, the cumulative distribution function F X F_X F X is defined asį X ( x ) = P ( X ≤ x ), F_X(x) = P(X \leq x), F X ( x ) = P ( X ≤ x ) ,


 0 kommentar(er)
0 kommentar(er)
